How much sod do I need?

How to measure the square footage of regular areas to be sodded.

Before ordering sod for your new lawn you must calculate the square footage of sod needed. To make the calculation simple, often this total can be reduced to a series of squares and rectangles. Using the following formula makes the task easy and gives you an accurate count of square feet needed.

 

1. Square or Rectangle

   Formula:
   Area = L x W
   A = Area
   L = Length
   W = Width

   Example:
   A = 90 feet x 50 feet
   A = 4,500 square feet

   The following illustration reduces the areas to be sodded around the house (A, B, C) and the backyard (D) to rectangles.

   

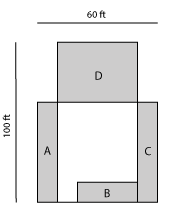
   Formula:
   Area A = 50’ x 10’ = 500 sq.ft.
   Area B = 30’ x 10’ = 300 sq.ft.
   Area C = 50’ x 1-‘ = 500 sq.ft.
   Area D = 40’ x 30’ = 1200 sq.ft.

   Example:
   Sod Needed: A (500 sq.ft.) + B (300 sq.ft.) + C (500 sq.ft.) + D (1,200 sq.ft.) = 2,500 sq.ft.

How to measure the square footage of irregular areas to be sodded.

Typically, you can reduce any irregularly shaped turf area to one or more geometric figures. You can then calculate the area of each figure and add the areas to obtain the total area. Irregular areas could include a pool, pond, garden, flower bed, tree area and so forth.

1. Ovals, Egg Shapes and Circles

   Ovals & Egg Shapes

   Formula:
   Area = 0.8 L x W
   A = Area
   L = Length
   W = Width at midpoint

   Example:
   A = 0.8 x 60 feet x 40 feet
   A = 1,920 square feet
   (within 5% accuracy)

   Circles

   Formula:
   Area =3.14 R²
   R = Radius

   Example:
   A = 3.14 x 30 feet x 30 feet
   A = 1,414 square feet

   The half circle backyard has a radius of 30 feet. A complete circle would be 302 or 3.14 x 30 ft. x 30 ft. = 2,826 sq.ft. Half would be 1,413 sq.ft.

   

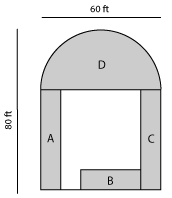
   Sod needed: A + B + C (1,300 sq.ft. – see page 1) + D (1,413 sq.ft.) = 2,713 sq.ft.

2. Irregular Shapes

   Formula:
   Measure the length of the longest axis across the area. Every 10 feet along the length , measure the width of the area at right angles to the length line. Total all widths and multiply by 10.

   Example:
   A = 40 ft. + 30 ft. + 50 ft. x 10
   A = 1200 square feet

   

   Sod Needed: A + B + C (1,300 sq.ft.) + D (see above) = 2,500 sq.ft.

3. Triangles

   Formula:
   Area = 0.5 x B x H
   A = Area
   B = Base
   H = Height

   Example:
   A = 0.5 x 25 ft. x 25 ft. = 312.5 sq.ft. x 2 (triangles) = 625 sq.ft.
   A = 625 sq.ft.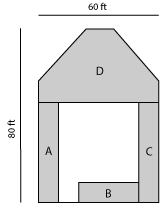

   

   Yard area D (below) is 60ft. x 40ft. = 2,400 sq.ft.
   Subtract the 2 triangles (625 sq.ft.)
   D = 2,400 sq.ft. – 625 sq.ft. = 1,775 square feet

   Sod Needed: A + B + B (1,300 sq.ft.) + D = 3,075sq.ft.

4. Trapezoid

   Formula:
   Area = 0.5 x (A + B) x H
   A = one parallel side
   B = second parallel side
   H = Height perpendicular to two parallel sides

   Example:
   Area = 0.5 x A + B (100 ft.) x H (30 ft.) = 1,500 sq.ft.

   

   Sod Needed: A + B + C (1,300 sq.ft.) + D = 2,800 sq.ft.

5. Unusual Shapes

   Formula:
   Divide area into sections of regular geometric shapes, calculate area of individual sections, then total

   Example:
   Triangle 0.5 x B (15ft.) x H (30 ft.) = 225 sq.ft.
   Rectangle 30 ft. x 45 ft. = 1,350 sq.ft.
   Circle (3.14) x 9 x 9 = 258 sq.ft. + 2 = 127 sq.ft.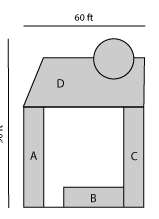

   

   Sod Needed: 225 sq.ft. + 1,350 sq.ft. + 127 sq.ft. = 1,702 sq.ft.